| Active Distributed Computing Projects - Mathematics |
|
These links take you to other project categories on this site:
Mathematics Language Art Puzzles/Games Miscellaneous Distributed Human Projects Collaborative Knowledge Bases Charity See the bottom of this page for a description of the icons on the page. |
| Project Information | Project % Complete | Major Supported Platforms | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 The current largest known Mersenne prime number is
277,232,917 - 1 (found on December 26, 2017, and containing
over 23 million digits). This is the largest known prime number and the 50th
Mersenne prime discovered (and the 16th Mersenne prime discovered by GIMPS).
Help find the next one in the
Great Internet Mersenne Prime Search
(GIMPS).
The 46th known Mersenne prime (and the 12th Mersenne prime discovered by GIMPS)
is 237,156,667 - 1 (found September 6, 2008, and containing 11.2
million digits).
The 47th known Mersenne prime (and the 13th Mersenne prime discovered by GIMPS)
is 242,643,801 - 1 (found April 12, 2009, and containing 12.8
million digits).
The 48th known Mersenne prime (and the 14th Mersenne prime discovered by GIMPS)
is 257,885,161 - 1 (found
January 25, 2013, and containing 17.4 million digits).
The 49th known Mersenne prime (and the 15th Mersenne prime discovered by GIMPS)
is 274,207,281 - 1 (found
January 7, 2016, and containing 22.3 million digits).
The 50th known Mersenne prime (and the 16th Mersenne prime discovered by GIMPS)
is 277,232,917 - 1 (found
December 26, 2017, and containing 23.2 million digits).
The current largest known Mersenne prime number is
277,232,917 - 1 (found on December 26, 2017, and containing
over 23 million digits). This is the largest known prime number and the 50th
Mersenne prime discovered (and the 16th Mersenne prime discovered by GIMPS).
Help find the next one in the
Great Internet Mersenne Prime Search
(GIMPS).
The 46th known Mersenne prime (and the 12th Mersenne prime discovered by GIMPS)
is 237,156,667 - 1 (found September 6, 2008, and containing 11.2
million digits).
The 47th known Mersenne prime (and the 13th Mersenne prime discovered by GIMPS)
is 242,643,801 - 1 (found April 12, 2009, and containing 12.8
million digits).
The 48th known Mersenne prime (and the 14th Mersenne prime discovered by GIMPS)
is 257,885,161 - 1 (found
January 25, 2013, and containing 17.4 million digits).
The 49th known Mersenne prime (and the 15th Mersenne prime discovered by GIMPS)
is 274,207,281 - 1 (found
January 7, 2016, and containing 22.3 million digits).
The 50th known Mersenne prime (and the 16th Mersenne prime discovered by GIMPS)
is 277,232,917 - 1 (found
December 26, 2017, and containing 23.2 million digits).
As of July 8, 2008, all exponents below 17,000,000 have been double-checked. As of July 4, 2008, all exponents below M(20996011) have been tested at least once. As of September 12, 2012, all exponents below M(43112609) have been tested at least once, all exponents below M(42643801) ihave been tested at least once, and all exponents below 25,000,000 have been double-checked. Unix users can participate in GIMPS using precompiled clients or source code at Ernst Mayer's site and the manual testing forms at the PrimeNet server. Clients can be downloaded from the project's download page. Version 27 of the Prime95 client is available for Windows 95/98/Me/NT/2000/XP/7 as of May 15, 2012. Version 24.14 or the mprime (or statically linked sprime) client is available for Linux and FreeBSD as of August 9, 2005. Clients are also available for Windows NT/2000/XP Service, OS/2, and Windows 3.1. See a complete list of features in these versions. See the download page for information about cliens for Apple/PowerPC, StrongARM, and UNIX machines. See the project's wiki. Join a discussion forum about this project. GIMPS also has a sub-project: ECM and P-1 Factoring. This project is "trying to factor numbers of the form 2N - 1 and 2N + 1 using either the P - 1 method or the Elliptic Curve Method (ECM)." On September 13, 2004, this project "found a 53-digit factor for M971. This was the smallest Mersenne number for which no factors were known!" |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
The OGR-NG project is finding optimal rulers for 26, 27, 28, and higher marks. It began work on OGR-26 in October, 2008, and completed work on the project on February 23, 2009. It verified that the current best 26-mark ruler was optimal. It began work on OGR-27 on February 23, 2009, and completed work on the project on February 24, 2014. Almost 20,000 volunteers helped verify that the best known ruler is optimal: 27/3-12-26-25-29-2-9-36-10-68-1-4-17-53-35-8-16-28-6-14-13-71-18-19-23-7 (length 553). Represented the other way, the ruler has marks at positions 0 3 15 41 66 95 97 106 142 152 220 221 225 242 295 330 338 354 382 388 402 415 486 504 523 546 553. The project tested 302,621,586 unique ruler stubs. It began work on OGR-28 on February 19, 2014. That project is still active. See the project's download page for the latest version of the client, and the project's pre-release page for versions which are available for testing before they become official versions. Use the RC5 key-rate calculator to see approximately what OGR node-rate your CPU will produce. The calculator was created by CalicoJak in January, 2003, and was last updated on February 22, 2006. |
OGR-28: ~1.54% in 5 days |
|
||||||||||||||||||||||||||||||||||||
|
Search for different kinds of prime numbers at Yves
Gallot's Proth Search Page.
Submit new primes to the Top 5000 Primes list. Version 7.1 of Proth is available as of May 4, 2010. As of January 19, 2010, the project has finished double-checking numbers for all k < 1,200 and n < 600,000. As of February 15, 2010, the project has extended its reservations to all k < 1,200 and n < 900,000. As of June 25, 2011, the project has finished double-checking numbers for all k < 1,200 and n < 1,000,000. As of August 25, 2011, the project has finished double-checking numbers for all k < 100 and n < 2,000,000. PrimeGrid will continue with k < 32 and n < 2,500,000. As of February 14, 2012, PrimeGrid has finished double-checking all k < 1200 and n < 1,500,000. As of February 29, 2008, the project is working with PrimeGrid. PrimeGrid will reserve large ranges of k and n and will complete its search of those ranges within two months. This project will not search those ranges while PrimeGrid has them reserved. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help find new factors of Cunningham numbers at ECMNET.
To participate in the project, download the client (available for Windows, Linux, Solaris and various other flavors of Unix), download the Cunningham input list (see the link on the project website), then run the client and report any factors it finds through a link on the project website. Version 2.7.0 of the ECMNet client/server is available as of December 3, 2005. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Find Minimal Equal
Sums of Like Powers using
Euler2000,
available on the download
page. The client automatically downloads ranges of numbers to work on. The
project celebrated its 10th anniversary on January 31, 2009. As of April 28,
2010 and the beginning of the yoyo@home Euler (6,2,5)
project, this project will continue to support participants running this client
but does not guarantee the project server may be available at all times to
accept results.
As of August, 2011, the project finished computing all solutions below 250,000. On February 6, 2003, a project member discovered the largest (6,2,5) result above 60,000. On December 8, 2002, a project member found a new upper limit for Taxicab(6): Taxicab(6) <= 24153319581254312065344, since 24153319581254312065344 = 289062063 + 5821623 = 288948033 + 30641733 = 286574873 + 85192813 = 270932083 + 162180683 = 265904523 + 174924963 = 262243663 + 182899223. The Taxicab problem isn't a part of the Minimal Equal Sums of Like Powers project, but this is a big discovery nonetheless. Version 4.21b of the client is available as of September 30, 2002. This version handles reserved work ranges better, points to the new eulernet.org domain automatically, and on the server side, allows for simultaneous client connections. Note: you should upgrade from version 4.18 and earlier to fix a significant client bug in those versions. Note: 4.21b has a bug which prevents the client from connecting to the server if you try to reserve more than the maximum 100 ranges. Use temporary version 4.21c to fix the bug. Note: the project server was switched to a new ISP and domain, eulernet.org, as of October 15, 2002. The client should use eulernet.org when trying to connect to the project server. If your client can't connect to the project server, try pressing Ctrl-U, then changing the server name from eulernet.org to euler.myip.org. This may solve your problem if the DNS is incorrect. Join a discussion forum about the project. |
ongoing: Resta 3 (6,1,6): 100.0% (completed October 23, 2002) Resta 6 (6,2,5): 90.47% |
|
||||||||||||||||||||||||||||||||||||
|
Search for factors of 2^(2^61-1)-1, a double Mersenne number, in the MM61 project. Download and test the client, then email the project coordinator to reserve a range of numbers to test.
Note that the project website is not accessible as of October 29, 2009. If you know of a new URL for the project or if the project has ended, please let me know. |
ongoing: 18,640 ranges done, 6,360 to do |
|
||||||||||||||||||||||||||||||||||||
 Find 3x+1 class records in the
3x+1 Problem
project. This project attempts to find ever higher 3x+1 class records.
The client, which will work on any PC/Windows platform, and the instructions
for joining the project, are
here.
Note: the client takes about 6 weeks to finish one block on a 400-MHz
CPU.
Find 3x+1 class records in the
3x+1 Problem
project. This project attempts to find ever higher 3x+1 class records.
The client, which will work on any PC/Windows platform, and the instructions
for joining the project, are
here.
Note: the client takes about 6 weeks to finish one block on a 400-MHz
CPU.
The project completed its first goal, processing 20,000 blocks, on November 19, 2002. The project found a new glide record in December, 2002. This is the first glide record found in almost a year. The record occurs at 180352,746940,718527, and the new glide is 1575, an improvement of 104 over the previous record. The project found a new Path record in March, 2003. The previous Path record was found in late 2002. The record occurs at 212581,558780,141311, (or +/- 189.250) and it reaches a maximum of 4353,436332,008631,522202,821543,171376. As of November 2, 2008, the project completed all blocks up to 67,500 and confirmed class record 2000. See the project's progress. |
ongoing: blocks to go to class record (unknown); all blocks up to 76,160 complete; all class records below 2,000 known |
|
||||||||||||||||||||||||||||||||||||
|
This site is also available in Italian See the project website for the latest version of the project's software clients. The mmff client, which is available as of October 1, 2012, uses GPU processing and is 50 times faster than any other program for Fermat and Double Mersenne numbers between F26 and F145. The project has found the following factors recently:
|
ongoing |
|
||||||||||||||||||||||||||||||||||||
 The
PCP@Home project looks for short cases of
Post's Correspondence
Problem with large
shortest solutions. This theoretical computer science problem has been in
existence since 1946. It demonstrates undecidability: "a problem that cannot
be solved for all cases by any algorithm whatsoever." Finding PCPs in this
project will help define "decidability criteria for bounded PCP classes."
The
PCP@Home project looks for short cases of
Post's Correspondence
Problem with large
shortest solutions. This theoretical computer science problem has been in
existence since 1946. It demonstrates undecidability: "a problem that cannot
be solved for all cases by any algorithm whatsoever." Finding PCPs in this
project will help define "decidability criteria for bounded PCP classes."
To participate in the project, download a precompiled, statically linked executable for Linux ELF, FreeBSD ELF, Solaris 5.6, or Windows (you can also download and compile the source code), and also download a perl script called PcpSieve.pl which runs the executable, scans the output for record solutions, and emails the solutions to the project coordinator (you can also run the executable manually, search the output manually and email any record solutions you find). Note to Windows users: the Windows client was compiled by Michael Keppler of Rechenkraft.net. He says that it has a serious memory leak, and that you may need to kill it and restart it every day. If anyone knows how to debug Windows application memory leaks, please contact him. This site is also available in German. |
possibly ended; Note: the project website has not been updated since 2004; the project may have ended |
|
||||||||||||||||||||||||||||||||||||
|
On January 6, 2003, Daniel Heuer discovered the largest known Generalized Fermat prime 148307665536+1 (404,434 digits), with GFNSieve+Proth, beating his previous record from October 8, 2002. "This number is the new largest known prime which is not a Mersenne prime, and the 6th largest known prime." On February 16, 2003, Michael Angel discovered the first prime of the form b217 + 1: 62722131072 + 1 (628,808 digits). This number is the 5th largest known prime. On February 21, 2003, the project completed the whole range 2-2,200,000 for exponent 32768. It found 35 primes in this range. On March 26, 2003, Franz Hagel discovered the 20th Generalized Fermat prime of the form b65536 + 1: 35786865536 + 1 (363,969 digits). On July 12, 2003, Michael Angel discovered the second known prime of the form b217 + 1: 130816131072 + 1. On August 22, 2003, Daniel Heuer discovered the largest known Generalized Fermat prime: 1176694217 + 1. This 795,695 digit number is now the 5th largest known prime. On September 22, 2003, Daniel Heuer discovered the new largest known Generalized Fermat prime: 1372930217 + 1. This 804,474 digit number is now the 5th largest known prime. On January 8, 2004, Yves Gallot discovered the 5th Generalized Fermat prime of the form b131072 + 1: 572186217 + 1 (754,652 digits). On May 30, 2004, Daniel Heuer discovered the two largest known Generalized Fermat primes: 1372930131072 + 1 (804,474 digits) and 1176694131072 + 1 (795,695 digits). Join a discussion forum about prime numbers. |
possibly ended;Note: the project website has not been updated since January, 2004; the project may have ended |
|
||||||||||||||||||||||||||||||||||||
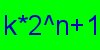 Help search for the 33rd largest prime number
in PSearch. A
Proth
prime is a prime number of the form
Help search for the 33rd largest prime number
in PSearch. A
Proth
prime is a prime number of the form Participants in the project should have at least a 600 Mhz PC. To join the project, first download George Woltman's PRP software for Windows or Linux. Then send email to William Garnett with your CPU type and speed and your operating system, and he will send you instructions for participating. Join a discussion forum about the project. |
24,092 of 37,328 candidates tested; should find one prime number in every 18,629 candidates; Note: the project website has not been updated since February, 2006; the project may have ended |
|
||||||||||||||||||||||||||||||||||||
 Help find the smallest
Sierpinski number in
Seventeen or Bust, a distributed attack on
the Sierpinski problem. The project looks for
Proth
prime numbers in which, for a number k, if every possible choice
of n results in a composite (non-prime) Proth number N,
k is a Sierpinski number.
Help find the smallest
Sierpinski number in
Seventeen or Bust, a distributed attack on
the Sierpinski problem. The project looks for
Proth
prime numbers in which, for a number k, if every possible choice
of n results in a composite (non-prime) Proth number N,
k is a Sierpinski number.
The project began its k=33661 project on November 21, 2002, and added fifteen additional projects on November 23, 2002. It has found the following primes:
The recent discovery of the 11th prime for the project helped prove a new mathematical theorem: the Mixed Sierpinski Problem. The results were published in a paper in the journal INTEGERS on December 23, 2008. To participate in the project, sign up for an account, download the client, add your account name to the client configuration, and run it. The client does Proth tests on individual numbers. Each number should take a few hours to test on an average machine. When the project server assigns you a number, it waits for up to 10 days for you to return your search results, and reassigns the number to someone else if it doesn't receive your results within that time. The client supports users behind firewalls and proxy servers. Version 28.5 of the client is available for Windows, Linux, Mac OSX and BSD as of July 7, 2014. Seventeen or Bust also has a supporting project to sieve numbers for the main project: sieving finds n numbers with small factors and removes them from the pool of prime number candidates which need to be tested by Seventeen or Bust. Two clients are available for sieving: SoBSieve (for Windows) and NBeGone (for multiple platforms). To reserve a range of numbers to sieve, post a message to the sieve coordination thread. Then submit the results from the range to the "sieve numbers" page mentioned above. The latest sob.dat file, with 10 k, is available as of January 3, 2005. As of January 9, 2005, users with regular user accounts can also perform second-pass tests of numbers the project has already tested once. This feature will be included in a future client, but for now it requires a bit of hacking for the Windows client. See details in this thread and participate at your own risk. See the project's Wiki. Join a discussion forum about the project. |
6 primes remaining to be found; 794,896 Proth tests completed |
|
||||||||||||||||||||||||||||||||||||
|
Find factorizations of cyclotomic numbers at
Factorizations
of Cyclotomic Numbers. This site doesn't appear to be
organized as an official distributed computing project and doesn't have
any precompiled client software or explicit instructions for participating,
so it is probably best suited for people who understand the Mathematical
principles behind the project and how to compile source code.
The Phi(92) series was completely factored by November 2, 2002: the last composite number was factored by Tetsuya Kobayashi on that date. Katsuyuki Okeya finished the Phi(61) and Phi(122) series on December 30, 2002. The Phi(69) series was completely factored by January 12, 2003: the last composite number was factored by Alexander Kruppa. The Phi(112) series is completely factored as of September 25, 2004. The Phi(144) series is completely factored as of October 12, 2004. The Phi(104) series is completely factored as of November 30, 2004. The Phi(168) series is completely factored as of December 24, 2004. The Phi(180) series is completely factored as of January 18, 2005. The Phi(65) series is completely factored as of February 9, 2005. The Phi(130) series is completely factored as of February 26, 2005. The Phi(156) series is completely factored as of March 6, 2005. The Phi(210) series is completely factored as of March 22, 2005. The Phi(53) series is completely factored as of July 1, 2006. The Phi(198) series is completely factored as of September 13, 2008. The Phi(118) series is completely factored as of September 22, 2008. To participate in the project, you can download and compile a GMP or UBASIC factorization program, view a page of reserved numbers, then select a range of numbers to factorize and send email to Hisanori Mishima with the range information. Read a paper about cyclotomic polynomials and prime numbers by Yves Gallot. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Join the
Goldbach Conjecture
Verification to help verify the conjecture through 1e18 (it is currently
verified through 1e16). The Goldbach conjecture is "one of the oldest
unsolved problems in number theory. ...it states that every even number
larger than two can be expressed as the sum of two prime numbers."
As of September 13, 2011, the project reached 26 . 1017. On November 30, 2011, the project discovered the minimal Goldbach partition 2795935116574469638=9629+P19. See all of the project's results. The client software consists of a server application which must be run on a GNU/Linux system with a version 2.4 or later kernel, and a client application which may be run on the same GNU/Linux system or on other GNU/Linux or Windows NT/2000/XP systems which can communicate with the server application over an intranet. As of May, 2005, "it is now possible to run the client program in "batch mode" in Windows. No server on GNU/Linux required. It will be necessary to manage things manually. The windows client program acts as a service. In particular, it does not run on a DOS windows. It runs invisibly in the background (at a very low priority)." To participate in the project, send email to Tomás Oliveira e Silva, the project coordinator, with information about the machine(s) on which you will run the server and client applications, and he will send you more information about how to participate. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help
The Riesel Problem project prove that k=509203 is the smallest
Riesel
Number. See the project's results on the
search status page.
To participate download the proth.exe client, view reserved ranges on the checked out and progress page, then reserve a range (and submit your results) on the range reservation page. The latest public Beta version of LLRNet is available as of April 5, 2004. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help find primes of the form 3 * 2n - 1
in the 3*2^n-1 Search.
This project builds on the work of the project
to find primes of the form k * 2n - 1 for k < 300. For
3 * 2n - 1, n is known up to 2,000,000. This project
is currently looking for new ns between 2,000,000 and 3,000,000. The
search to n=2,000,000 (about 600,000 digits) was completed on July
1, 2005. As of March 12, 2007, candidates have been sieved to 245 trillion,
6,958 total candidates are ready for LLR testing, and 119 work blocks are
available for LLR testing.
The project has found the following primes recently:
To participate, download one of the following software clients: LLR, PFGW, PRP (see download links in the discussion forum), then reserve a range from the 3-4M reservations page and download a zip file of all the input files from a link on that page. After you run the client, email the results to Paul Underwood. Version 3.7.1 of LLR (available here) is available as of May 4, 2006. The latest sieved files are available as of February 23, 2007. Join a discussion forum about the project. |
87.54% for n up to 1,000,000 digits |
|
||||||||||||||||||||||||||||||||||||
|
Join the
Search
for Multifactorial Primes. This project continues work started by
Ray Ballinger to find multifactorial prime numbers, primes of the form
n!!+/-1, n!!!+/-1, n!!!!+/-1, searching for all primes
up to 10,000 digits for each multifactorial type.
The project has recently proven the following numbers are prime:
On March 29, 2005, the project finished !19 to 200,000. On May 31, 2005, the project finished !17 + 1 to 170,000. On August 6, 2005, the project finished !17 - 1 to 170,000. On August 21, 2005, the project finished !25 to 200,000. On September 9, 2005, the project finished !15 to 130,000. On November 26, 2005, the project finished !15 to 150,000. On November 26, 2005, the project tested all types up to 20 to 10,000 * type +/- 1. On December 20, 2005, the project finished !3 + 1 to 75,000. On February 28, 2006, the project finished !24 + 1 to 240,000. On March 27, 2008, the project finished !25 + 1 to 250,000. On July 8, 2010, the project finished !12 - 1 to 160,000. Participation instructions are at the top of the project page. Basically, you email the project coordinator to reserve a type, then use the multisieve and pfgw Windows applications to sieve the range and find primes in it, then submit your results to the project coordinator. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
 Find factors of the Mersenne number
M(3326400) = 23326400 - 1 in
ElevenSmooth. Note:
this project is active, but the project website is not updated unless a major
event occurs. The website was last updated on November 8, 2012. See the
project's completed factorizations.
Find factors of the Mersenne number
M(3326400) = 23326400 - 1 in
ElevenSmooth. Note:
this project is active, but the project website is not updated unless a major
event occurs. The website was last updated on November 8, 2012. See the
project's completed factorizations.
On February 1, 2004 the project "found a 42 digit factor of M(5280) using GMP-ECM with B=3M. This is expected to qualify for 9th place in Paul Zimmerman's Top Ten This Year list." On April 4, 2004, the project found P35, the first known primitive factor of M(15840). On May 14, 2004, the project found P34, the second known factor of M(10395). On June 9, 2004, the project found P25, the second known factor of the primitive part of M(66528). On June 12, 2004, the project found a P49 factor for M(1485), the largest factor found by ElevenSmooth using ECM. On July 20, 2004, the project completed the factorization of M(3960). On September 18, 2004, the project found a P28 factor of M(95040): this is the first known factor of the primitive part of M(95040). On October 19, 2004, the project found a P36 factor of M(11880), "the second known factor for the primitive part of this number." On July 28, 2005, the project found a P35 factor of M(47520), the third factor the project has found for the primitive part of M(47520). In early December, 2005. the project found a 41-digit factor of M(6336). In March, 2008, the project completed the factorization of M(1575). On May 7, 2008, the project completed the factorization of M(2376). On July 16, 2008, the project found a P34 factor of M(5400) (using ECM at the B1=1M level). This factor reduces the unfactored residual from C406 to C373. This is the second factor ElevenSmooth has found for this number. On November 15, 2008, the project found a P37 factor of M(100800). This factor reduces the unfactored residual from C6925 to C6889. On March 27, 2009, the project found a P51 factor of 23360 + 1. This is the largest factor ElevenSmooth has found by ECM and is the fourteenth primitive for which ElevenSmooth has completed the factorization. See news of more recent factor discoveries on the project's main page. To participate in the project, download the ECMclient application and configure it according to the directions on the download page (if you already have the ECM or ECMclient application installed, you only need to reconfigure it to use server=wblipp.dynu.com and port=8194). Unix users can follow instructions to create an ECM client for Unix. Once ECMclient is configured, it contacts the ElevenSmooth project server to get work units and to return results. It processes a work unit for 30 minutes by default, but you can change the processing time by changing the maxfreq parameter. The project supports users behind firewalls and possibly proxy servers. It supports modem users with a little bit of work. See the help page for information about using firewalls, proxy servers, and modems. The project also has a Special Project sub-project for users who have contributed at least one full week to the main ECM project. The Special Project "uses GIMPS' program Prime95 to work on all primitives of M(3326400) simultaneously. If any ECM work is going to be done on the largest composites, Prime95 is much faster. The subfactor composites are then tested 'for free.' However, even with Prime95, it takes a long time to run ECM curves on large numbers." Users who qualify for this project will be invited by email to join it. See the project's progress and completed factorizations. Join a discussion forum about the project. |
unknown |
|
||||||||||||||||||||||||||||||||||||
 Help
The Prime Sierpinski Project
find the smallest prime
Sierpinski number. "The smallest known prime Sierpinski number is
k=271129. Finding a prime of type k * 2n + 1 for all prime
k < 271129 will be sufficient to prove that 271129 is the smallest prime
Sierpinski number." As of January 2, 2005, 24 k have been eliminated and 7 k
remain to be tested. It is currently searching the following k: 79309,
79817, 90527, 152267, 156511, 168451, 222113, 225931, 237019, 258317.
Help
The Prime Sierpinski Project
find the smallest prime
Sierpinski number. "The smallest known prime Sierpinski number is
k=271129. Finding a prime of type k * 2n + 1 for all prime
k < 271129 will be sufficient to prove that 271129 is the smallest prime
Sierpinski number." As of January 2, 2005, 24 k have been eliminated and 7 k
remain to be tested. It is currently searching the following k: 79309,
79817, 90527, 152267, 156511, 168451, 222113, 225931, 237019, 258317.
The project's first anniversary was on November 8, 2004. By that date it eliminated 11 k's by finding 11 large primes, and also sieved to almost 40 trillion. In the next year it hopes to reach at least n=2.5 million for PRP, to find serveral new primes, and to sieve to 100 trillion. As of October 1, 2005, it has tested all n below n=1600000 at least once. With help from PrimeGrid, the project's sieve entered the 10P range by September 30, 2008. The project has found the following prime numbers recently:
To participate in the project, read the Getting Started discussion thread, then download and run the network LLR client. The client automatically reserves work units and submit results. Join a discussion forum about this project. |
7 k remaining; untested pairs up to n=50,000,000 |
|
||||||||||||||||||||||||||||||||||||
 Help
P.I.E.S (Prime Internet
Eisenstein Search) find large prime
Generalised
Eisenstein Fermat numbers numbers. The project's main goal is to study
the properties of these numbers, and for that it needs to find some prime
numbers.
Help
P.I.E.S (Prime Internet
Eisenstein Search) find large prime
Generalised
Eisenstein Fermat numbers numbers. The project's main goal is to study
the properties of these numbers, and for that it needs to find some prime
numbers.
To participate in the project, send email to the project owner, user "thefatphil" at host "yahoo.co.uk", to let him know you're interested. Then download the client and follow the instructions on the download page for running it. Version 0.7 of the client is available for Windows. Version 0.8 is available for Linux, FreeBSD, AIX and Irix. |
ongoing; Note: the project website has not been updated since 2005 and may be inactive |
|
||||||||||||||||||||||||||||||||||||
|
Help find
Factors of k*2^n±1 for k=3,5,7,9,11,13 and N < 1000.
See the 50 most recent factors. As of September 5, 2004, the project has reached n=500 for all k=11. The project now includes numbers for k=13, also factored up to n=500. "Numbers for k=13, n > 500 have had very little ecm done on them." The doecm client downloads composites and submits results automatically, but you can manually reserve numbers and submit factors through the website. Version 1.01 of the client is available for Windows and Linux. You can also download and compile the source code for the client. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help factor numbers of the form
xy + yx in the
XYYXF project.
The project completed the factorization of all numbers with y < 11 as of February 7, 2005. It completed the factorization of all numbers up to x = 90 as of March 16, 2005. It completed the factorization of all numbers with y < 16 as of April 27, 2005. The number of composites was reduced to 2500 as of September 10, 2005. It completed the factorization of all numbers with y <= 100 as of October 28. The number of composites was reduced to 2300 as of October 18, 2007. It completed the factorization of all numbers up to x = 100 as of October 28, 2007. The number of composites was reduced to 1800 as of November 25, 2009. The number of composites was reduced to 1300 as of June 26, 2012. The project added a Primes and PRPs of the form xy + yx page to its website on June 6, 2008. The project has factored the following numbers recently:
The project has also factored the following numbers recently:
You can reserve numbers manually through the project website and factor them with your favorite factoring client application (GMP-ECM is reocmmended), or you can use the ECMclient application and automatically reserve numbers and submit results (use the ecmserver childers.myip.org, port 34). Version 6.0 of GMP-ECM is available as of February 28, 2005. Version 2.5.6 of ECMclient is available as of March 16, 2005. Version 1.50 of MSieve, another client which can be used for the project, is available as of February 3, 2012. As of November 19, 2004, there are 3,242 XYYXF composites from C93 to C321. 761 of them are reserved; 2,481 (including 123 more wanted) are available. Due to a massive SNFS attack, only 38 new numbers were added to the "most wanted" list for 2005. As of June 26, 2012, 1,300 composites are left. As of November 12, 2012, no composites are left which have fewer than 154 digits. Join a Yahoo! Group discussion forum about this project. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help search for a billion-digit Mersenne prime in
Operation Billion Digits. The project website is also available
in Italian
To participate in the project, download Luigi Morelli's factor3_2.exe client and some Cygwin files from the project web page, then reserve an unassigned exponent in the project's discussion forum. Version 2 of the client is currently available. It is 25% faster than the previous version. Join a discussion forum about this project. See the project's latest progress updates. |
ongoing; currently at level 12.00 (9 candidates trial factored to 74 bits) |
|
||||||||||||||||||||||||||||||||||||
|
Help
Primesearch find primes of the form k *
2n - 1. The project is currently searching k between 301-399
with n at least 16001.
To participate in the project, sign up for an account on the website, then reserve ranges and submit results through the website. Use either the proth or primeform application: links to these applications are on Prime Links++ to process your reserved ranges. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Lone
Mersenne Hunters looks for Mersenne prime numbers which
have not been tested by other projects or by GIMPS'
Primenet server.
To participate, read the instructions in the How to start? discussion thread. Note: this project only has a discussion forum and no website. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Factoring
is a collection of factoring projects.
Factoring completed the factorization of 2^791+1 (to 45 digits) on May 2, 2005. It completed the factorization of 2,1342L on May 8, 2005. It achieved a new P - 1 record, 2,2098M c281 = p58 * c224, on September 28, 2005. Factoring Projects:
To participate, read the instructions in the forum. Note: these projects only have a discussion forum and no websites. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help the
100 Million digits prefactor project
remove exponents which can be factored now from
GIMPS' search for the first known 100 million digit prime
number. This is a sister project to
Operation Billion
Digits. The project does "wide" prefactoring, in which it prefactors
"large ranges of exponents [at a depth of no less than 50 bits and no more
than 55 bits] to eliminate large numbers of exponents," and "deep"
prefactoring, in which it prefactors "individual exponents to higher bit
depths, usually into the mid 60's (possibly higher)." As of January 21, 2009,
the project has deep prefactored to bit depths as high as 77.
To participate in the project, download Luigi Morelli's factor3_2.exe client and some Cygwin files, or Mfactor for win32, or 32-bit or 64-bit Linux, from links on the project web page. (See more information in the guide.) Then look for an available range or exponent in the table on the project web page and follow the instructions on the project web page to reserve the range or exponent and to submit results. Version 2 of the factor3_2 client is currently available. It is 25% faster than the previous version. Join a discussion forum or a mailing list about this project. |
ongoing0 exponents factored--> |
|
||||||||||||||||||||||||||||||||||||
|
Help
Repdigit Prime Problems find prime numbers of the form n * k, where k is a single
digit which can be repeated any number of times (for example, for n = 47
and k = 3, a possible repdigit prime might be 473333).
To participate in the project, use the primeform application (follow the directions on the project page for using primeform), and send email to the project coordinator to reserve a range to check and to submit results. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help
Mersenneplustwo Factorization factor numbers of the form 2^p+1.
To participate in the project, use one of the software clients listed on the project website. The project website does not contain details about how to use the clients or about how to reserve numbers and submit results. More information may be available in the project's discussion forum. Also see the project's wiki. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help
Sierpinski/Riesel Base 5 for the smallest base 5 Sierpinski and Riesel numbers. The project
does not have a website, only a discussion forum.
The project has found the following primes recently:
To participate in the project, use NewPGen to sieve and PRP to test, and follow these instructions. As of October 15, 2006, a Linux version of the LLRNet client is available from http://base5.greenbank.org/. See instructions for using this client. Note that the reservation list reached the 10,000 character limit on October 15, 2005, so participants should follow the links to the sieve files on the reservations page. |
ongoing |
|
||||||||||||||||||||||||||||||||||||

The project passed 1 TeraFLOPS/second of computing power on February 27, 2006. On September 12, 2006, the project began a new test project called SZTAKI Desktop Grid Research Facility (szdgr). This project will "improve the testing process of applications, thus improving user-experience (get rid of the credit problems, etc.) of SZTAKI Desktop Grid." The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. Version 2.01 of the project's NumSys Search client is available for Windows as of October 16, 2006. Version 2.03 is available for Linux as of August 1, 2006. Version 2.00 is available for Mac OSX as of July 5, 2006. Join a discussion forum about the project. |
temporarily closed; 163,931,407 credits |
|
||||||||||||||||||||||||||||||||||||
|
On February 28, 2007, the project reported its 100th prime to the prime pages. On November 26, 2006, the project began working with Twin Internet Prime Search, and is supporting a second sub-project to help that project. It completed its search on August 6, 2009, with the discovery of twin primes. On October 3, 2008, the project achieved "'optimal' sieve depth [in the Cullen/Woodall project] ...actually, a little beyond it. Therefore, we are stopping the 32 bit and 64 bit Cullen/Woodall Sieve applications and archiving the sieve. Cullen/Woodall LLR will remain active up to n=10M. For more information, please see this forum post." On December 27, 2008, the project began a new sub-project, AP26 Search, "an Arithmetic Progression of 26 primes. An arithmetic progression of primes is a sequence of primes with a common difference between any two successive numbers in the sequence. For example 3, 7, 11 is an arithmetic progression of 3 primes with a common difference of 4." On August 8, 2008, the project announced a "Dog Days of Summer Challenge." The three-day challenge ran from August 22-24 and supported PrimeGrid's 321 Prime Search LLR application. See more information in a forum thread about the challenge. On September 6, 2008, the project announced a "Back to the Future Challenge." The 14-day challenge ran from September 13-27 and supported the Woodall Prime Search for the next record Woodall prime. During the challenge, "over 8,000 Woodall [work units] were completed by 204 teams and 1108 individuals." See more information in the challenge's forum thread. On January 24, 2009, the project announced a "Year of the Ox Challenge." The 5-day challenge supported the project's 321 Prime Search (LLR) sub-project. See more information in the challenge's forum thread. The project began its Tour de Primes 2009 contest on February 1, 2009. On February 14, 2009, the project announced a partnership with 12121 Search. On April 20, 2009, the project's Cullen Prime Search found a World Record Cullen Mega Prime: 6328548 * 26328548 + 1 (1,905,090 digits). At that time this prime was the largest Cullen prime found and the largest Mega Prime found using LLR. On August 6, 2009, the project's Cullen Prime Search found its next World Record Cullen Mega Prime: 6679881 * 26679881 + 1 (2,010,852 digits). The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. Version 5.13 of the project's Prime Generator client is available as of May 16, 2006. Version 5.04 of the project's LLR Prime Search client is available as of November 25, 2006. Join a discussion forum about this project. |
1,558,626,413 credits |
|
||||||||||||||||||||||||||||||||||||
Help find Riesel primes, primes of the form k * 2n - 1, with k > 1, in the
Riesel Prime Search.
This project has three sub-projects:
See the latest primes found by the project here and here. To participate, look for (or ask for) instructions in the project forums. Note: this project only has a discussion forum and no website. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
 Help
Rectilinear Crossing Number
determine "the least number of crossings for a straight-edge drawing of the
complete graph on top of a set of n points in a plane." See
more information about
the project. The project is currently focusing on n=18. The project website
is also available in Russian
and German.
Help
Rectilinear Crossing Number
determine "the least number of crossings for a straight-edge drawing of the
complete graph on top of a set of n points in a plane." See
more information about
the project. The project is currently focusing on n=18. The project website
is also available in Russian
and German.
On May 21, 2008 the project began releasing W7 work units. The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. Version 5.45 of the project's CAPE Crossing Number client is available for Linux as of August 3, 2006. Version 5.41 is available for Windows as of July 4, 2006. Version 5.49 of the project's TCAPE Crossing Number client is available for Linux and Windows as of August 5, 2006. Join a discussion forum about the project. |
8,222,202 credits |
|
||||||||||||||||||||||||||||||||||||
 Help
ABC@home find abc triples for the
ABC Conjecture,
"one of the greatest open problems in mathematics." "abc triples are positive
integers a,b,c such that a+b = c, a < b < c, a,b,c have no common
divisors and c > rad(abc), the so-called radical of abc. The ABC conjecture
says that there are only finitely many a,b,c such that log(c) / log(rad(abc))
> h for any real h > 1. ... If i[the conjecture] is proven to be true,
a lot of other open problems can be answered directly from it." The project
completed its first major goal in Janaury, 2009, and will restart in February,
2009, with a new, better algorithm and new work units.
Help
ABC@home find abc triples for the
ABC Conjecture,
"one of the greatest open problems in mathematics." "abc triples are positive
integers a,b,c such that a+b = c, a < b < c, a,b,c have no common
divisors and c > rad(abc), the so-called radical of abc. The ABC conjecture
says that there are only finitely many a,b,c such that log(c) / log(rad(abc))
> h for any real h > 1. ... If i[the conjecture] is proven to be true,
a lot of other open problems can be answered directly from it." The project
completed its first major goal in Janaury, 2009, and will restart in February,
2009, with a new, better algorithm and new work units.
The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. Version 1.00 of the project's ABC finder client is available for Windows and Linux as of January 13, 2007. Join a discussion forum about the project. |
101,152 credits |
|
||||||||||||||||||||||||||||||||||||
|
Help the
WEP-M+2 Project find
factors of Mersenneplustwo numbers. "Mersenneplustwo numbers are those
integers that are two more than a Mersenne prime. Mersenne primes are of the
form 2^p-1 (see Mersenne Prime Search).
This makes Mersenneplustwo numbers of the form 2^p+1."
The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. Version 1.06 of the project's "Random-base WEP Factorization" client is available for Linux/x86 as of January 4, 2007. Version 1.07 of the client is available for Linux/AMD64 as of January 21, 2007. Version 1.04 of the client is available for Mac OSX as of December 5, 2006. Join a discussion forum about the project. |
unknown credits |
|
||||||||||||||||||||||||||||||||||||
 yoyo@home OGR is
a BOINC-based wrapper for
distributed.net's
OGR-25 project.
yoyo@home OGR is
a BOINC-based wrapper for
distributed.net's
OGR-25 project.
The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. Version 1.08 of the project's Cruncher application is available for Windows as of September 2, 2007. Version 1.07 is available for Linux/X86 as of August 30, 2007. Version 1.08 is available for Linux/X86-64 as of October 2, 2007. Version 1.07 is available for Mac OSX as of August 31, 2007. Version 1.08 is available for Solaris and FreeBSD as of September 30, 2007. Version 1.09 is available for PS3 as of September 30, 2007. Join a discussion forum about yoyo@home. |
70,543,602 credits for all yoyo@home projects |
|
||||||||||||||||||||||||||||||||||||
 Help Wieferich@Home
find Wieferich primes. Only two Wieferich primes are known: 1093 and 3511.
See more information
about the project.
Help Wieferich@Home
find Wieferich primes. Only two Wieferich primes are known: 1093 and 3511.
See more information
about the project.
To participate in the project, download and run the project's software client. Version 2.0 of the client is available for Windows as of February 4, 2008. This version "accelerates searching in complete and periodical test. Software makes use of totally new algorithms, which are very efficient for mathematical method: exponentiation and congruency. New units for complete test are 10x larger and in periodical test 1.5x larger." Join a discussion forum about this project. |
0 Wieferich primes found |
|
||||||||||||||||||||||||||||||||||||
|
Help No Prime Left Behind
find Riesel primes of the form k *
2n - 1 for 300 < k <= 1001 and 1400 < k < 3000
and not reserved by others or actively being worked on.
To participate in the project, follow instructions in the project's Software/instructions/questions discussion thread. The project uses the LLR, NewPGen, Sr1sieve, Sr2sieve, Srfile, and Srsieve applications. Join a discussion forum about this project. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help k6465
find primes of the form 6465 * 2n - 1.
To participate in the project, send email to the project owner to reserve a range, then download NewPGen version 2.82 for pre-sieveing and LLR version 3.71c for finding primes (you can download these applications from http://gbarnes017.googlepages.com/primebehindprogs.zip or from links listed in other projects above), then search for prime numbers within that range, then email the results to the project owner. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Help NFS@Home
complete the
lattice sieving
step of number field sieve
factorizations of large integers. The project is currently working on
Cunningham
composites.
The project factored M1061 (P143 * P177) on August 4, 2012. The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. See the project's Applications page for information about the client applications and versions the project is using. Join a discussion forum about this project. |
unknown credits |
|
||||||||||||||||||||||||||||||||||||
 yoyo@home ECM is supporting several projects which use Elliptic Curve Factorization
to find factors for different kinds of numbers.
yoyo@home ECM is supporting several projects which use Elliptic Curve Factorization
to find factors for different kinds of numbers.
On August 29, the project found an unusually large P62 factor to finish its 853^73 - 1 project. The factor was found with the B1=11e6 curve, which is "optimal for finding 45-digit factors." The factor is one of the 50 largest ECM factors ever found. "It is both a Brent composite and a Mishima Cyclotomic Number." See the project's progress page for its latest results. The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. See the project applications page for the latest version of the ECM client. Join a discussion forum about yoyo@home. |
567,135,297 credits for all yoyo@home projects as of May 6, 2010 |
|
||||||||||||||||||||||||||||||||||||
 yoyo@home Euler (6,2,5) is searching for minimal equal sums of power 6. The project
expects to find at least 32 new sums. See more information about the project.
yoyo@home Euler (6,2,5) is searching for minimal equal sums of power 6. The project
expects to find at least 32 new sums. See more information about the project.
The project finished on June 8, 2010. The project began another Euler625 project on June 12, 2010. This project is expected to end in September, 2011. See the latest solutions found by the project. The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. See the project applications page for the latest version of the Euler (6,2,5) client. Join a discussion forum about yoyo@home. |
10.2% |
|
||||||||||||||||||||||||||||||||||||

The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. See the project's applications page for the latest version of the Separator client. Join a discussion forum about the project. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
The project uses a BOINC-based client. See the BOINC platform information for the latest version of the BOINC client. See the project's applications page for the latest version of the project's application clients. See more information about the project's application clients. Join a discussion forum about the project. |
ongoing |
|
||||||||||||||||||||||||||||||||||||
|
Minimal Superpermutation Problem is looking for minimal superpermutations, "strings formed from a set of n symbols such that every one of the n! permutations of those symbols appears at least once as a contiguous block of n characters in the string." It is using a distributed Chaffin method to perform its search and is tracking its efforts in the Distributed Chaffin Method Results page. See a current summary of the project's efforts on the Distributed Chaffin Method Results page. As of March 17, 2020, the project is "searching for strings consisting of digits between 1 and 6 that contain as many permutations as possible, while 'wasting' only 119 digits. By a 'wasted' digit, we mean one that, when added to the string, did not add a (new) permutation. We don’t count the first 5 digits as wasted." To participate in the project download the project software from the project's GitHub repository, then read the README file in the repository for instructions for using the software. Register for access to the Superpermutators Google group to see the project's latest news and discuss the project's results. |
ongoing |
|
| The following icons may appear in the Supported Platforms section of the table: | |||||||||||||
|
| Top... |