| Project Information | Project % Complete | Major Supported Platforms | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mathematics | ||||||||||||||||||||
The current largest known Mersenne prime number is
213,466,917 - 1 (found on November 14, 2001, and containing
4,053,946 digits). Help find the next one in the
Great Internet Mersenne Prime
Search (GIMPS).Unix users can participate in GIMPS using precompiled clients or source code at Ernst Mayer's site and the manual testing forms at the PrimeNet server. Version 22.12 of the client is available as of November 9, 2002. Note: semi-serious bugs were discovered in versions 22.10 and 22.11, so please upgrade your client if you are using either of those versions. Join a discussion group about this project. The group is hosted by Team Prime Rib, but is open to everyone. |
ongoing |
|
||||||||||||||||||
|
Search for different kinds of prime numbers at Yves Gallot's Proth Search Page. Submit new primes to the Top 5000 Primes list. Version 7.1 of Proth is available as of October 29, 2002. See the list of prime numbers that I've found. |
ongoing |
|
||||||||||||||||||
| Help find new factors of Cunningham numbers at ECMNET. | ongoing |
|
||||||||||||||||||
| Search for the next prime of the form n!+1 (or of the form n!-1) using primeform. You can reserve and submit ranges for either project through the website. | ongoing |
|
||||||||||||||||||
|
Find Minimal Equal
Sums of Like Powers using
Euler2000,
available on the download
page. The client automatically downloads ranges of numbers to work on.
On December 13, 2002, a project member discovered the largest (6,2,5) result: 599956 + 68566 = 579746 + 412506 + 393726 + 155406 + 94996. On December 8, 2002, a project member found a new upper limit for Taxicab(6): Taxicab(6) <= 24153319581254312065344, since 24153319581254312065344 = 289062063 + 5821623 = 288948033 + 30641733 = 286574873 + 85192813 = 270932083 + 162180683 = 265904523 + 174924963 = 262243663 + 182899223. The Taxicab problem isn't a part of the Minimal Equal Sums of Like Powers project, but this is a big discovery nonetheless. Version 4.21b of the client is available as of September 30, 2002. This version handles reserved work ranges better, points to the new eulernet.org domain automatically, and on the server side, allows for simultaneous client connections. Note: you should upgrade from version 4.18 and earlier to fix a significant client bug in those versions. Note: the project server's old ISP and domain (euler.myip.org) are unreachable as of October 15, 2002. Please use the domain eulernet.org. |
ongoing: Resta 3 (6,1,6): 100.0% (completed October 23, 2002) Resta 6 (6,2,5): 59.05% |
|
||||||||||||||||||
Search for K-optimal lattice rules in GRISK.
The client will work behind a firewall if your firewall lets through traffic on port 5060/tcp, or if you have a SOCKS firewall. To run it behind a SOCKS firewall, run it with options like the following: java -DsocksProxyHost=<host> -DsocksProxyPort=<port:default=1080> jistributed.JistributedClient krypvier.ii.uib.no A Windows client is available as of November 6, 2000. A Macintosh OS X client is also available. The client is available for many other Unix platforms. The Delta=7 project was completed on November 15, 2000. The Delta=8 project was completed on December 21, 2001. The Delta=11 project began on December 21, 2001. |
d=11: 20.6% |
   
|
||||||||||||||||||
| Search for factors of 2^(2^61-1)-1, a double Mersenne number, in the MM61 project. Download and test the client, then email the project coordinator to reserve a range of numbers to test. | ongoing: 6,253 ranges done, 1,747 to do |
|
||||||||||||||||||
Find 3x+1 class records in the
3x+1 Problem
project. This project attempts to find ever higher 3x+1 class records.
The client, which will work on any PC/Windows platform, and the instructions
for joining the project, are
here.
Note: the client takes about 6 weeks to finish one block on a 400-MHz
CPU.
The project completed its first goal, processing 20,000 blocks, on November 19, 2002. The project found a new glide record in December, 2002. This is the first glide record found in almost a year. The record occurs at 180352,746940,718527, and the new glide is 1575, an improvement of 104 over the previous record. See the project's progress. |
ongoing |
|
||||||||||||||||||
|
The
pi(x) project calculates pi(x), for very large values of x. It most
recently calculated pi(x) for x=4*1022. You can
contribute to the calculations for pi(x) for x=1023.
Version 1.5 of the client is available as of February 17, 2001. The project is on hold as of April 15, 2002, while a problem in the software is resolved. |
on hold |
|
||||||||||||||||||
|
Help the Distributed Search for Fermat Number Divisors project find unique Fermat Number factors.
This site is also available in Italian Version 4.1 of the client is available as of September 7, 2001. The latest factor, 51.2282719 + 1 divides F282717, the third-largest known Fermat factor with 85,109 digits, was discovered by Kevin Odermatt on November 13, 2002. 242 total Fermat factors are known: 8 have been found in 2002. Join the project discussion group or an independent discussion group about Fermat numbers. |
ongoing |
|
||||||||||||||||||
The
PCP@Home project looks for short cases of
Post's Correspondence
Problem with large
shortest solutions. This theoretical computer science problem has been in
existence since 1946. It demonstrates undecidability: "a problem that cannot
be solved for all cases by any algorithm whatsoever." Finding PCPs in this
project will help define "decidability criteria for bounded PCP classes."
To participate in the project, download a precompiled, statically linked executable for Linux ELF, FreeBSD ELF, Solaris 5.6, or Windows (you can also download and compile the source code), and also download a perl script called PcpSieve.pl which runs the executable, scans the output for record solutions, and emails the solutions to the project coordinator (you can also run the executable manually, search the output manually and email any record solutions you find). Note to Windows users: the Windows client was compiled by Michael Keppler of Rechenkraft.net. He says that it has a serious memory leak, and that you may need to kill it and restart it every day. If anyone knows how to debug Windows application memory leaks, please contact him. This site is also available in German. |
ongoing |
|
||||||||||||||||||
Find generalized Fermat prime numbers in the
Generalized Fermat Prime Search. This project uses the
Proth program or the
GFNSieve21 program to find these numbers. Unix-users and other users
can compile the
C source code of "GeneFer" for the project and you can directly check
a pre-sieved range with
it. Version 1.2 of this code is available as of June 10, 2002.
On October 8, 2002, Daniel Heuer "discovered the largest known Generalized Fermat prime 147803665536+1 (404,337 digits), with GFNSieve+Proth. This number is the new largest known prime which is not a Mersenne prime, and the 6th largest known prime." Join a discussion group about prime numbers. |
ongoing |
|
||||||||||||||||||
Find generalized Woodall numbers in the
Generalized
Woodall Numbers project. This project uses the Proth program to find these numbers.
|
ongoing |
|
||||||||||||||||||
|
Help find strong pseudoprimes. From the project
website:
A composite odd integer x is a base b strong pseudoprime if by=1 (mod x) or there exists a r such that 0 <= r < t and by2r= -1 (mod x) where x-1=y2t and y is odd. Setup of the client is straightforward, but not trivial. Be sure to read the README file. |
ongoing |
|
||||||||||||||||||
|
Help find Wilson primes. From the project
website:
An odd prime p is a wilson prime if (p-1)!+1=0 mod p2. The only known wilson primes are 5, 13, and 563. Setup of the client is straightforward, but not trivial. Be sure to read the README file. |
ongoing |
|
||||||||||||||||||
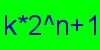Help
search for the world's largest Proth prime number. A
Proth
prime is a prime number of the form Participants in the project should have at least a 600 Mhz PC. To join the project, first download George Woltman's PRP software for Windows or Linux. Then send email to William Garnett with your CPU type and speed and your operating system, and he will send you instructions for participating. |
ongoing |
|
||||||||||||||||||
|
Help
search for Wieferich
prime numbers, numbers of the form ap-1 = 1
(mod p2) for a = 2 or 3. The only two known Wieferich primes
are 1,093 and 3,511 and there are no other Wieferich primes less than
2 * 1014. This project hopes to extend the search limit to
at least 2 * 1015.
The client automatically reserves ranges to check from the project server, and returns its results when it is done checking the ranges. It runs as a screen-saver for Windows and as a command-line client for Linux/Solaris. It only works on computers with full-time Internet connections. The Windows client supports users behind firewalls: the Unix clients currently do not, but will in a future release. |
ongoing: 98,279 ranges checked; 128 near misses found |
|
||||||||||||||||||
Help find the smallest
Sierpinski number in
Seventeen or Bust, a distributed attack on
the Sierpinski problem. The project looks for
Proth
prime numbers in which, for a number k, if every possible choice
of n results in a composite (non-prime) Proth number N,
k is a Sierpinski number.
The project began its k=33661 project on November 21, 2002, and fifteen additional projects on November 23, 2002. It has found the following primes:
To participate in the project, sign up for an account, download the client, add your account name to the client configuration, and run it. The client does Proth tests on individual numbers. Each number should take a few hours to test on an average machine. When the project server assigns you a number, it waits for up to two weeks for you to return your search results, and reassigns the number to someone else if it doesn't receive your results within that time. The client supports users behind firewalls and proxy servers. Version 1.0.0 of the client is available for Windows as of November 18, 2002. This version includes many new features. Version 1.0.2 is available for Linux, BeOS and FreeBSD as of November 27, 2002. Note: as of October 5, 2002, results from version 0.9.0 or earlier of the client are not accepted by the server. Please upgrade if you are running an older version. Windows users with dual-CPU machines can download a special copy of the 0.9.9 Windows client which will allow them to run the client on both CPUs. |
12 primes remaining to be found; 54,691 Proth tests completed |
|
||||||||||||||||||
|
Find factorizations of
cyclotomic
numbers at
Factorizations of Cyclotomic Numbers. This site doesn't appear to be
organized as an official distributed computing project and doesn't have
any precompiled client software or explicit instructions for participating,
so it is probably best suited for people who understand the Mathematical
principles behind the project and how to compile source code.
As of November 2, 2002, the Phi(92) series has been completed factored: the last composite number was factored by Tetsuya Kobayashi on that date. To participate in the project, you can download and compile a GMP or UBASIC factorization program, view a page of reserved numbers, then select a range of numbers to factorize and send email to Hisanori Mishima with the range information. Read a paper about cyclotomic polynomials and prime numbers by Yves Gallot. |
ongoing |
|
||||||||||||||||||
|
Help find prime numbers for
the dual Sierpinski problem
search. The project is trying to find a prime in each sequence of
integers of the form k+2n (fixed k) for which no prime has yet
been found. The project is coordinated by Payam Samidoost, an active
researcher of Fermat numbers. Contact Payam to reserve numbers to check
and to submit your results.
The project uses George Woltman's PRP software (available for Windows and Linux). Instructions for downloading and using the software are listed here. |
ongoing |
|
||||||||||||||||||
|
Discover Lychrell numbers in the
Lychrell Challenge (the
actual challenge is described
here). A Lychrell
number is a number that does not form a palindrome by reversing and adding
its digits. The project began as a
search for a
palindrome for 196 (no palindrome has yet been found). A distributed
client for the project should be available in the next few months, but
for now you can download a standalone client from a link on the
File Verification
page and search for numbers independently. You can report any numbers
you find to Wade VanLandingham, the project coordinator, and he will add
them to the records
page. The project FAQ has a
good summary of information about the project.
See the latest news about the project. |
ongoing: 31,714 numbers found; 152,601,888 iterations; 62,163,113 digits |
|
||||||||||||||||||
Help verify Riemann's hypothesis in
ZetaGrid. This
hypothesis was formulated in 1859 and states that "all non-trivial zeros of
the Riemann zeta function (see the website) are on the critical line
(1/2+it where t is a real number)." No one has been able
to prove the hypothesis in 140 years. It is now considered one of
the most important problems of modern mathematics. The project offers
financial prizes.
See close
zeros found by the project.
The client runs as a Windows screensaver or service or as a command-line application. The command-line version displays a configurable amount of information about what it is doing. You must have Java Runtime Environment 1.2.2 or higher installed to use the client. It only needs to be connected to the Internet to receive work or send results. Version 1.7.1 of the client is available as of December 27, 2002. A Control Center client is also available for Windows: it allows you to monitor multiple CPUs and estimates the time remaining to complete an active work unit. Note to users of the command-line client. You must download both the zeta_base.zip and zeta_platform.zip files to use this version of the client. Edit zeta.cfg to specify your user information and how you want the client to use your system. Next, download the zeta.cmd or zeta.sh startup script and edit it to define your JAVA_HOME and proxy server (if you have one) variables. See research papers about this project and its results. |
ongoing: 220 billion results returned |
|
||||||||||||||||||
|
Join the
Goldbach Conjecture
Verification to
help verify the conjecture through 1e18 (it is currently verified
through 1e16). The Goldbach conjecture is "one of the oldest unsolved problems
in number theory. ...it states that every even number larger than two can be
expressed as the sum of two prime numbers."
The client software consists of a server application which must be run on a GNU/Linux system with a version 2.4 or later kernel, and a client application which may be run on the same GNU/Linux system or on other GNU/Linux or Windows NT/2000/XP systems which can communicate with the server application over an intranet. To participate in the project, send email to Tomás Oliveira e Silva, the project coordinator, with information about the machine(s) on which you will run the server and client applications, and he will send you more information about how to participate. |
ongoing |
|
||||||||||||||||||
|
Help the
pi(x) Table Project construct a very large table of values of pi(x) for
large values of x. The table will allow people to study the behavior of
the pi(x) function in large ranges, a study which has never before been
possible. The project might also find the first known change of sign of the
function pi(x)-Li(x). The first phase of the project computed pi(x) for
1.e16 < x < 1.e17. The current phase is computing pi(x) for 1.e17 <
x < 1.e18.
To participate in the project, download the DOS executable fastpix11.exe from the project website, reserve ranges of numbers through the website, process the ranges, and submit your results to the website. You may reserve a range for no longer than two weeks. |
unknown |
|
||||||||||||||||||
 
Help find difference triangles with the smallest
(optimal) span for a given sequence in the Triangles project. The project
doesn't have a website, but will have one soon. The project evolved from a
programming contest, sponsored by Al Zimmerman, which ran from July, 2002
to October 15, 2002. See the
final results of the contest. The project uses a modified version of
Jean-Charles Meyrignac's client for the
Minimal Equal Sums of Like Powers
project and a modified version of Stephen Montgomery-Smith's
Dispense Package distributed
computing platform.
See the smallest known spans discovered by the project. To participate, download and run a Windows client. Instructions for using the client can be found in the archives of the discussion group below. Source code for the client is also available for download. Version 1.12 of the client is available as of December 7, 2002. Note: this project is still in development. If you decide to participate, please be aware that the client and probably the project will change frequently. Join a discussion group about the project. |
ongoing: 561,437 entries submitted |
|
||||||||||||||||||
, 
, and 
.
