| Active Distributed Computing Projects - Mathematics |
|
These links take you to other project categories on this site:
Mathematics Art Puzzles/Games Miscellaneous Distributed Human Projects Collaborative Knowledge Bases Charity See the bottom of this page for a description of the icons on the page. |
| Project Information | Project % Complete | Major Supported Platforms | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mathematics | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 The current largest known Mersenne prime number is
224,036,583 - 1 (found on May 15, 2004, and containing
7.2 million digits). This is the largest known prime number. Help find the
next one in the Great Internet Mersenne Prime
Search (GIMPS).
The current largest known Mersenne prime number is
224,036,583 - 1 (found on May 15, 2004, and containing
7.2 million digits). This is the largest known prime number. Help find the
next one in the Great Internet Mersenne Prime
Search (GIMPS).Unix users can participate in GIMPS using precompiled clients or source code at Ernst Mayer's site and the manual testing forms at the PrimeNet server. The 41st known Mersenne Prime was reported on May 15, 2004: the number will be announced in mid-June, after it is verified. Version 23.8 of the client is available for Windows as of February 17, 2004. Version 23.5 of the client is available for Linux and FreeBSD as of July 3, 2003. See a complete list of features in these versions. Join a discussion group about this project. GIMPS also has a sub-project: ECM and P-1 Factoring. This project is "trying to factor numbers of the form 2N - 1 and 2N + 1 using either the P - 1 method or the Elliptic Curve Method (ECM)." On September 13, 2004, this project "found a 53-digit factor for M971. This was the smallest Mersenne number for which no factors were known!" |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Search for different kinds of prime numbers at Yves Gallot's Proth Search Page. Submit new primes to the Top 5000 Primes list. Version 7.1 of Proth is available as of December 10, 2004.
|
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help find new factors of Cunningham numbers at ECMNET.
To participate in the project, download the client (available for Windows, Linux, Solaris and various other flavors of Unix), download the Cunningham input list (see the link on the project website), then run the client and report any factors it finds through a link on the project website. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Find Minimal Equal
Sums of Like Powers using
Euler2000,
available on the download
page. The client automatically downloads ranges of numbers to work on.
On February 6, 2003, a project member discovered the largest (6,2,5) result above 60,000. On December 8, 2002, a project member found a new upper limit for Taxicab(6): Taxicab(6) <= 24153319581254312065344, since 24153319581254312065344 = 289062063 + 5821623 = 288948033 + 30641733 = 286574873 + 85192813 = 270932083 + 162180683 = 265904523 + 174924963 = 262243663 + 182899223. The Taxicab problem isn't a part of the Minimal Equal Sums of Like Powers project, but this is a big discovery nonetheless. Version 4.21b of the client is available as of September 30, 2002. This version handles reserved work ranges better, points to the new eulernet.org domain automatically, and on the server side, allows for simultaneous client connections. Note: you should upgrade from version 4.18 and earlier to fix a significant client bug in those versions. Note: 4.21b has a bug which prevents the client from connecting to the server if you try to reserve more than the maximum 100 ranges. Use temporary version 4.21c to fix the bug. Note: the project server's old ISP and domain (euler.myip.org) are unreachable as of October 15, 2002. Please use the domain eulernet.org. |
ongoing: Resta 3 (6,1,6): 100.0% (completed October 23, 2002) Resta 6 (6,2,5): 70.95% |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Search for factors of 2^(2^61-1)-1, a double Mersenne number, in the MM61 project. Download and test the client, then email the project coordinator to reserve a range of numbers to test. | ongoing: 8,572 ranges done, 1,428 to do |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Find 3x+1 class records in the
3x+1 Problem
project. This project attempts to find ever higher 3x+1 class records.
The client, which will work on any PC/Windows platform, and the instructions
for joining the project, are
here.
Note: the client takes about 6 weeks to finish one block on a 400-MHz
CPU.
Find 3x+1 class records in the
3x+1 Problem
project. This project attempts to find ever higher 3x+1 class records.
The client, which will work on any PC/Windows platform, and the instructions
for joining the project, are
here.
Note: the client takes about 6 weeks to finish one block on a 400-MHz
CPU.
The project completed its first goal, processing 20,000 blocks, on November 19, 2002. The project found a new glide record in December, 2002. This is the first glide record found in almost a year. The record occurs at 180352,746940,718527, and the new glide is 1575, an improvement of 104 over the previous record. The project found a new Path record in March, 2003. The previous Path record was found in late 2002. The record occurs at 212581,558780,141311, (or +/- 189.250) and it reaches a maximum of 4353,436332,008631,522202,821543,171376. See the project's progress. |
ongoing: all blocks up to 41,080 complete; all class records below 1,900 known |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help the Distributed Search for Fermat Number Divisors project find unique Fermat Number factors.
This site is also available in Italian Version 4.1 of the client is available as of September 7, 2001. A new factor, 89.2472,099 + 1 divides F472,097 was discovered by Payam Samidoost on October 5, 2004. This is the third-largest Fermat factor known. Another new factor, 211.2287,388 + 1 divides F287,384 was discovered by Jim Fougeron on December 13, 2004. Join the project discussion group or an independent discussion group about Fermat numbers. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 The
PCP@Home project looks for short cases of
Post's Correspondence
Problem with large
shortest solutions. This theoretical computer science problem has been in
existence since 1946. It demonstrates undecidability: "a problem that cannot
be solved for all cases by any algorithm whatsoever." Finding PCPs in this
project will help define "decidability criteria for bounded PCP classes."
The
PCP@Home project looks for short cases of
Post's Correspondence
Problem with large
shortest solutions. This theoretical computer science problem has been in
existence since 1946. It demonstrates undecidability: "a problem that cannot
be solved for all cases by any algorithm whatsoever." Finding PCPs in this
project will help define "decidability criteria for bounded PCP classes."
To participate in the project, download a precompiled, statically linked executable for Linux ELF, FreeBSD ELF, Solaris 5.6, or Windows (you can also download and compile the source code), and also download a perl script called PcpSieve.pl which runs the executable, scans the output for record solutions, and emails the solutions to the project coordinator (you can also run the executable manually, search the output manually and email any record solutions you find). Note to Windows users: the Windows client was compiled by Michael Keppler of Rechenkraft.net. He says that it has a serious memory leak, and that you may need to kill it and restart it every day. If anyone knows how to debug Windows application memory leaks, please contact him. This site is also available in German. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On January 6, 2003, Daniel Heuer discovered the largest known Generalized Fermat prime 148307665536+1 (404,434 digits), with GFNSieve+Proth, beating his previous record from October 8, 2002. "This number is the new largest known prime which is not a Mersenne prime, and the 6th largest known prime." On February 16, 2003, Michael Angel discovered the first prime of the form b217 + 1: 62722131072 + 1 (628,808 digits). This number is the 5th largest known prime. On February 21, 2003, the project completed the whole range 2-2,200,000 for exponent 32768. It found 35 primes in this range. On March 26, 2003, Franz Hagel discovered the 20th Generalized Fermat prime of the form b65536 + 1: 35786865536 + 1 (363,969 digits). On July 12, 2003, Michael Angel discovered the second known prime of the form b217 + 1: 130816131072 + 1. On August 22, 2003, Daniel Heuer discovered the largest known Generalized Fermat prime: 1176694217 + 1. This 795,695 digit number is now the 5th largest known prime. On September 22, 2003, Daniel Heuer discovered the new largest known Generalized Fermat prime: 1372930217 + 1. This 804,474 digit number is now the 5th largest known prime. On January 8, 2004, Yves Gallot discovered the 5th Generalized Fermat prime of the form b131072 + 1: 572186217 + 1 (754,652 digits). On May 30, 2004, Daniel Heuer discovered the two largest known Generalized Fermat primes: 1372930131072 + 1 (804,474 digits) and 1176694131072 + 1 (795,695 digits). Join a discussion group about prime numbers. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
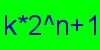 Help search for the 17th largest prime number
in PSearch. A
Proth
prime is a prime number of the form
Help search for the 17th largest prime number
in PSearch. A
Proth
prime is a prime number of the form Participants in the project should have at least a 600 Mhz PC. To join the project, first download George Woltman's PRP software for Windows or Linux. Then send email to William Garnett with your CPU type and speed and your operating system, and he will send you instructions for participating. Join a discussion group about the project. |
14,058 of 37,328 candidates tested; should find one prime number in every 18,629 candidates |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Help find the smallest
Sierpinski number in
Seventeen or Bust, a distributed attack on
the Sierpinski problem. The project looks for
Proth
prime numbers in which, for a number k, if every possible choice
of n results in a composite (non-prime) Proth number N,
k is a Sierpinski number.
Help find the smallest
Sierpinski number in
Seventeen or Bust, a distributed attack on
the Sierpinski problem. The project looks for
Proth
prime numbers in which, for a number k, if every possible choice
of n results in a composite (non-prime) Proth number N,
k is a Sierpinski number.
The project began its k=33661 project on November 21, 2002, and fifteen additional projects on November 23, 2002. It has found the following primes:
To participate in the project, sign up for an account, download the client, add your account name to the client configuration, and run it. The client does Proth tests on individual numbers. Each number should take a few hours to test on an average machine. When the project server assigns you a number, it waits for up to 10 days for you to return your search results, and reassigns the number to someone else if it doesn't receive your results within that time. The client supports users behind firewalls and proxy servers. Version 2.2 of the client is available for Windows, Linux, FreeBSD, and BeOS as of December 11, 2004. Seventeen or Bust also has a supporting project to sieve numbers for the main project: sieving finds n numbers with small factors and removes them from the pool of prime number candidates which need to be tested by Seventeen or Bust. Two clients are available for sieving: SoBSieve (for Windows) and NBeGone (for multiple platforms). To reserve a range of numbers to sieve, post a message to the sieve coordination thread. Then submit the results from the range to the "sieve numbers" page mentioned above. Join a discussion forum about the project. |
11 primes remaining to be found; 324,812 Proth tests completed |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Find factorizations of cyclotomic numbers at
Factorizations
of Cyclotomic Numbers. This site doesn't appear to be
organized as an official distributed computing project and doesn't have
any precompiled client software or explicit instructions for participating,
so it is probably best suited for people who understand the Mathematical
principles behind the project and how to compile source code.
The Phi(92) series was completely factored by November 2, 2002: the last composite number was factored by Tetsuya Kobayashi on that date. Katsuyuki Okeya finished the Phi(61) and Phi(122) series on December 30, 2002. The Phi(69) series was completely factored by January 12, 2003: the last composite number was factored by Alexander Kruppa. The Phi(112) series was completely factored by September 25, 2004. The Phi(144) series was completely factored by October 12, 2004. The Phi(104) series was completely factored by November 30, 2004. To participate in the project, you can download and compile a GMP or UBASIC factorization program, view a page of reserved numbers, then select a range of numbers to factorize and send email to Hisanori Mishima with the range information. Read a paper about cyclotomic polynomials and prime numbers by Yves Gallot. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The client runs as a Windows screensaver or service or as a command-line application. The command-line version displays a configurable amount of information about what it is doing. You must have Java Runtime Environment 1.2.2 or higher installed to use the client. It only needs to be connected to the Internet to receive work or send results. Version 1.9.3 of the client is available as of August 18, 2004. A Control Center client is also available for Windows: it allows you to monitor multiple CPUs and estimates the time remaining to complete an active work unit. The ZetaGrid library 0140 is available as of April 18, 2004. Note to users of the command-line client. You must download both the zeta_base.zip and zeta_platform.zip files to use this version of the client. Edit zeta.cfg to specify your user information and how you want the client to use your system. Next, download the zeta.cmd or zeta.sh startup script and edit it to define your JAVA_HOME and proxy server (if you have one) variables. See research papers about this project and its results. |
ongoing: 996.6 billion results returned |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Join the
Goldbach Conjecture
Verification to
help verify the conjecture through 1e18 (it is currently verified
through 1e16). The Goldbach conjecture is "one of the oldest unsolved problems
in number theory. ...it states that every even number larger than two can be
expressed as the sum of two prime numbers."
The client software consists of a server application which must be run on a GNU/Linux system with a version 2.4 or later kernel, and a client application which may be run on the same GNU/Linux system or on other GNU/Linux or Windows NT/2000/XP systems which can communicate with the server application over an intranet. To participate in the project, send email to Tomás Oliveira e Silva, the project coordinator, with information about the machine(s) on which you will run the server and client applications, and he will send you more information about how to participate. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help
The Riesel Problem project prove that k=509203 is the smallest
Riesel
Number. See the project's results on the
search status page.
To participate download the proth.exe client, view reserved ranges on the checked out and progress page, then reserve a range (and submit your results) on the range reservation page. The latest public Beta version of LLRNET is available as of April 5, 2004. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help find primes of the form 3 * 2n - 1
in the 3*2^n-1 Search.
This project builds on the work of the project
to find primes of the form k * 2n - 1 for k < 300. For
3 * 2n - 1, n is known up to 164,987. This project
is currently looking for new ns between 191,600 and 2,000,000. As of
December 10, 2004, the search to n=2,000,000 (about 600,000 digits)
is 43.7% complete, candidates have been sieved to 70 trillion (about 14
digits), 13,364 total candidates are ready for LLR testing, and 223 work
blocks are available for LLR testing.
The project has found the following primes recently:
To participate, download one of the following software clients: LLR, PFGW, PRP (see download links in the discussion forum) and send email to Paul Underwood. He will send you instructions on how to participate and will give you blocks to process. Version 2.2 of LLR2 (available here for Athlons and other non-SSE2 computers) is available as of November 14, 2004. Note: this project only has a discussion forum and no website. |
38.9% for n=2 million (about 600,000 digits) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 NFSNET uses "the
Number Field Sieve to find the factors of increasingly large numbers."
You can participate in the project by following the instructions on the
join page. See the project's
latest news.
NFSNET uses "the
Number Field Sieve to find the factors of increasingly large numbers."
You can participate in the project by following the instructions on the
join page. See the project's
latest news.
On November 10, 2002, NFSNET completed the factorization of W(668), a 204-digit special number field sieve (SNFS). The client is command-line, with a GUI wrapper client available. It is better for users with permanent Internet connections. It supports users behind firewalls but not users behind proxy servers. Release Candidate 1 of the client is available as of May 12, 2003. The project's 10 most recent factorizations:
Join a discussion forum about the project. Subscribe to the project mailing list. |
5307 - 1: 30.9% complete |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Join the
Search
for Multifactorial Primes. This project continues work started by
Ray Ballinger to find multifactorial prime numbers, primes of the form
n!!+/-1, n!!!+/-1, n!!!!+/-1, searching for all primes
up to 10,000 digits for each multifactorial type.
The project has recently proven the following numbers are prime:
On April 18, 2004, the project finished !20 to 200,000. On April 28, 2004, the project finished !16 to 160,000. On May 4, 2004, the project finished !13 to 130,000. On May 11, 2004, the project finished !3-1 to 57,500. On August 25, 2004, the project finished !5-1 to 100,000. On October 26, 2004, the project finished !18 to 180,000. On October 31, 2004, the project finished !25 to 180,000. On November 16, 2004, the project finished !23 to 100,000. On November 18, 2004, the project finished !11 to 250,000. Participation instructions are at the top of the project page. Basically, you email the project coordinator to reserve a type, then use the multisieve and pfgw Windows applications to sieve the range and find primes in it, then submit your results to the project coordinator. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
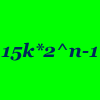 Help find primes of the form 15k *
2n - 1 in the
15k Prime Search. The project is looking for 15k which produce many primes
n: "in general when k has many small factors, n is more likely to
produce a prime because it cant have those same factors."
Help find primes of the form 15k *
2n - 1 in the
15k Prime Search. The project is looking for 15k which produce many primes
n: "in general when k has many small factors, n is more likely to
produce a prime because it cant have those same factors."
The project has found the following prime numbers recently:
See the primes the project has found. To participate, follow the instructions on the main HowTo page or the Phase 2 - HowTo page. Version 3.3 of the llrp4 client is available for Windows and Linux as of November 30, 2004. Join a discussion forum about the project. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Find factors of the Mersenne number
M(3326400) = 23326400 - 1 in
ElevenSmooth.
Find factors of the Mersenne number
M(3326400) = 23326400 - 1 in
ElevenSmooth.
On February 1, 2004 the project "found a 42 digit factor of M(5280) using GMP-ECM with B=3M. This is expected to qualify for 9th place in Paul Zimmerman's Top Ten This Year list." On April 4, 2004, the project found P35, the first known primitive factor of M(15840). On May 14, 2004, the project found P34, the second known factor of M(10395). On June 9, 2004, the project found P25, the second known factor of the primitive part of M(66528). On June 12, 2004, the project found a P49 factor for M(1485), the largest factor found by ElevenSmooth using ECM. On July 20, 2004, the project completed the factorization of M(3960). On September 18, 2004, the project found a P28 factor of M(95040): this is the first known factor of the primitive part of M(95040). On October 19, 2004, the project found a P36 factor of M(11880), "the second known factor for the primitive part of this number." To participate in the project, download the ECMclient application and configure it according to the directions on the download page (if you already have the ECM or ECMclient application installed, you only need to reconfigure it to use server=wblipp.dynu.com and port=8194). Unix users can follow instructions to create an ECM client for Unix. Once ECMclient is configured, it contacts the ElevenSmooth project server to get work units and to return results. It processes a work unit for 30 minutes by default, but you can change the processing time by changing the maxfreq parameter. The project supports users behind firewalls and possibly proxy servers. It supports modem users with a little bit of work. See the help page for information about using firewalls, proxy servers, and modems. The project also has a Special Project sub-project for users who have contributed at least one full week to the main ECM project. The Special Project "uses GIMPS' program Prime95 to work on all primitives of M(3326400) simultaneously. If any ECM work is going to be done on the largest composites, Prime95 is much faster. The subfactor composites are then tested 'for free.' However, even with Prime95, it takes a long time to run ECM curves on large numbers." Users who qualify for this project will be invited by email to join it. See the project's progress and completed factorizations. Join a discussion forum about the project. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Help the
Riesel Sieve's efforts to solve the
Riesel problem by
"removing prime candidates for the remaining 81 k's from a huge .dat file....
The .dat file contains n values from a current low of about 400,000 to a high
of 20,000,000 per remaining k. Individual sieving efforts per single k can
take two weeks to a month to sieve to a sufficient level. This coordinated
sieving effort will allow us to sieve 100 times deeper and much quicker. No
more sieving to 3T and stopping in frustration as the hours per factor mount,
now we can go to 300T and beyond..." Before the project began, there were 101
candidate k's and over 11 million k/n pairs. See the
status of all remaining k
values. See an overview
of the tests remaining to be completed.
Help the
Riesel Sieve's efforts to solve the
Riesel problem by
"removing prime candidates for the remaining 81 k's from a huge .dat file....
The .dat file contains n values from a current low of about 400,000 to a high
of 20,000,000 per remaining k. Individual sieving efforts per single k can
take two weeks to a month to sieve to a sufficient level. This coordinated
sieving effort will allow us to sieve 100 times deeper and much quicker. No
more sieving to 3T and stopping in frustration as the hours per factor mount,
now we can go to 300T and beyond..." Before the project began, there were 101
candidate k's and over 11 million k/n pairs. See the
status of all remaining k
values. See an overview
of the tests remaining to be completed.
As of November 17, 2004, the project has sieved all of its ks to 75T. The project has found the following prime numbers recently:
To participate in the project, use the LLRNET client to automatically download ranges of numbers and to submit results (see instructions for using it), or view instructions on the download page to use the rieselsiexe.exe client. Basically you download the rieselsieve.exe executable and the riesel.dat data file (about 6 MB compressed and 27 MB fully expanded). Then you reserve a range of numbers, process them with rieselsieve.exe, and submit your resulting factors. The riesel.dat file is updated regularly and gets smaller as prime candidates are removed. Version 0.42 of the Proth_sieve client is available for Windows and Linux as of February 12, 2004. This version is 5-10% faster than the previous version. A client should be available for FreeBSD soon. The latest version of LLRNET is available as of May 24, 2004. The riesel.dat file was last updated on December 21, 2004. Join a discussion forum about the project. |
220,271 LLR tests completed |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Help
The Prime Sierpinski Project
find the smallest prime
Sierpinski number. "The smallest known prime Sierpinski number is
k=271129. Finding a prime of type k * 2n + 1 for all prime
k < 271129 will be sufficient to prove that 271129 is the smallest prime
Sierpinski number." As of June 28, 2004, 17 k have been eliminated and 15 k
remain to be tested.
Help
The Prime Sierpinski Project
find the smallest prime
Sierpinski number. "The smallest known prime Sierpinski number is
k=271129. Finding a prime of type k * 2n + 1 for all prime
k < 271129 will be sufficient to prove that 271129 is the smallest prime
Sierpinski number." As of June 28, 2004, 17 k have been eliminated and 15 k
remain to be tested.
The project's first anniversary was on November 8, 2004. By that date it eliminated 11 k's by finding 11 large primes, and also sieved to almost 40 trillion. In the next year it hopes to reach at least n=2.5 million for PRP, to find serveral new primes, and to sieve to 100 trillion. The project has found the following prime numbers recently:
To participate in the project, read the Getting Started discussion thread, then download and run the network LLR client. The client automatically reserves work units and submit results. Join a discussion group about this project. |
15 k remaining; 927,261 untested pairs up to n=20,000,000 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Help
P.I.E.S (Prime Internet
Eisenstein Search) find large prime
Generalised
Eisenstein Fermat numbers numbers. The project's main goal is to study
the properties of these numbers, and for that it needs to find some prime
numbers. Note that the project owner has blocked the website from viewers
in the US, the UK, Australia, Denmark, and other countries which "support
the US's war on Iraq." If you are in one of these countries you will not be
able to see the project site, but will instead see a page of political
protest information. You can contact the owner to have your IP address
unblocked.
Help
P.I.E.S (Prime Internet
Eisenstein Search) find large prime
Generalised
Eisenstein Fermat numbers numbers. The project's main goal is to study
the properties of these numbers, and for that it needs to find some prime
numbers. Note that the project owner has blocked the website from viewers
in the US, the UK, Australia, Denmark, and other countries which "support
the US's war on Iraq." If you are in one of these countries you will not be
able to see the project site, but will instead see a page of political
protest information. You can contact the owner to have your IP address
unblocked.
See the project's results. To participate in the project, send email to the project owner, user "thefatphil" at host "yahoo.co.uk", to let him know you're interested. Then download the client and follow the instructions on the download page for running it. Version 0.7 of the client is available for Windows. Version 0.8 is available for Linux, FreeBSD, AIX and Irix. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help find
Factors of k*2^n±1 for k=3,5,7,9,11,13 and N < 1000.
See the 50 most recent factors. As of September 5, 2004, the project has reached n=500 for all k=11. The project now includes numbers for k=13, also factored up to n=500. "Numbers for k=13, n > 500 have had very little ecm done on them." The doecm client downloads composites and submits results automatically, but you can manually reserve numbers and submit factors through the website. Version 1.01 of the client is available for Windows and Linux. You can also download and compile the source code for the client. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help factor numbers of the form
xy + yx in the
XYYXF project.
The project has factored the following numbers recently:
You can reserve numbers manually through the project website and factor them with your favorite factoring client application, or you can use the ECMclient application and automatically reserve numbers and submit results (use the ecmserver childers.myip.org, port 34). As of November 19, 2004, there are 3,242 XYYXF composites from C93 to C321. 761 of them are reserved; 2,481 (including 123 more wanted) are available. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help the 12121
Search find large primes of the form 121 * 2n - 1,
a subsidiary of the search of k * 2n - 1 for
k < 300. This project plans to search for n up to 1,000,000 in the short
term, and for larger n in the long term.
The project has found the following prime numbers recently:
To participate in the project, download the LLR.exe client from a link on the project web page, then reserve a range on the project page. When the test is complete, submit the results on the project page. A new LLR.exe client was released on August 2, 2004: it appears to work faster than the old LLR.exe on SSE2 Systems (P4 and AMD64) and slower on non-SSE2 systems. Join a discussion forum about this project. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help search for a billion-digit Mersenne prime in
Operation Billion Digits. The project website is also available
in Italian
To participate in the project, download Luigi Morelli's factor3_2.exe client and some Cygwin files from the project web page, then reserve an unassigned exponent in the project's discussion forum. Version 2 of the client is currently available. It is 25% faster than the previous version. Join a discussion forum about this project. |
ongoing; currently at level 6.5 (6 candidates trial factored to 72 bits and all candidates without a factor to at least at 66 bits) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help
SIGPS (The Small
Internet GFN Prime Search) search for primes of the form b8192 + 1
(b > 99999999), a Generalized Fermat prime number. The project uses
the AthGFNsv.exe client to sieve candidate primes. The project started
looking for primes of the form b16384 + 1 on December 2, 2004.
To participate in the project, follow the directions on the project page for downloading and running the command-line client. The client is based on Yves Gallot's genefer program. It does not appear to support users behind proxy servers. The client automatically downloads work from the project server and submits results to the project server. Version 1.6 of the client is available for Linux as of November 26, 2004. The client's source code is available for download. The project has found the following prime numbers recently:
|
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Help Primesearch find primes of the form k * 2n - 1. The project is currently searching k between 301-399 with n at least 16001. To participate in the project, sign up for an account on the website, then reserve ranges and submit results through the website. Use either the proth or primeform application: links to these applications are on Prime Links++ to process your reserved ranges. |
ongoing |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The following icons may appear in the Supported Platforms section of the table: | |||||||||||||
|
| Top... |